競技プログラミングを布教したい

※この記事は「eeic2022 Advent Calendar 2021」の16日目の記事の一本目（！？）です、二本目についてはこちらをご覧ください（二本目は競技プログラミングとは関係ない記事です）。
※割と学科民向けに書いてるので具体的な講義名とかが出てきて外部の人には優しくない記事かもしれませんがご了承ください。

０. 自己紹介

何気にeeic内定してからここで記事書くの初めてでは？なわけで改めて、東京大学（まだ）理科一類のモグリン（AtCoder ID: mogurin）と申します。一応競プロの記事だしいつもの貼っておくとこんな感じ。




ん？君停滞してない？というかHeatMapの右側真っ白なんだけど......
はい、実は競プロサボりまくっててコンテストも出てないことがしばしば、いや、中間試験とシャニマスとルペルカリアがね......

やっぱ学科民の中に私より強い人もめちゃめちゃいそうだししかも競プロについて書く人既にいるんごじゃん、私がわざわざ競プロについて書く必要ないな！解散！！......と思ってたんですけどね、とある理由により書くモチベが生えたので私も書きます、ちなみにAPG4bからAtCoderへの導線を張ろうとした記事を過去に書いてるのでこっちも読んでね！（宣伝は基本）

１. そもそものお話

競プロってなにそれおいしいの？みたいな人は流石にいないと思いますがまあ一応ざっくり書くとこの記事で扱うAtCoderのように専用のコンテストにてプログラミングを用いて問題を解く（入力に対して要求された出力を返すプログラムを書く）、パズルのような遊びです（ちょくだいさん曰くネトゲ）。特徴としてはゴリゴリ数百行のプログラムを書く開発とは違い、あくまでも問題を解けるアルゴリズムを考えて実装するのが目的なのでそこまで重実装にならないことが多いです（もちろん例外もあるし難易度の高い問題程実装量は上がる）。その分短時間で適切なアルゴリズムを考え出さなければいけなく、特に計算量という概念が競プロにおいては超重要になってくるのですが、いかにして計算量を減らしたアルゴリズムを考え出せるかが競プロにおける醍醐味と言えるでしょう。この辺の面白さを短時間で知りたいならkort0nさんの記事がおススメです。

２. 結局何が楽しいの？

競プロの楽しみ方は結構人によって異なるため一概に「これが楽しくてこう楽しむのが正解！」みたいにいうことはできません、ここから書くことはあくまで私個人の感想であるためご了承ください。

１. 正解（AC）の快感

頑張って書いたコードが通った瞬間の気持ちよさが異常、ソフⅠの自動採点で祈ってた人はわかるはず。

２. 色んなアルゴリズムを知ることが出来る

競技プログラミング、最近はそこそこ競技人口多めなので色んな人が記事を書いてくれてるし最近はわかりやすい記事も大量に出回っています、割とよく使うアルゴリズムなら問題解いてわかんないワード調べてるだけでサクサク身につくのが楽しいです、特に演習教材となる問題にその場で取り組めるのも魅力的。余談ですが簡単なもののなかではめぐる式二分探索初めて知った時は感動しました、中の人誰だかわからないけどすごい。
twitter.com

【めぐるのアルゴリズム講座】
二分探索（整数）の書き方
難しさ：４ pic.twitter.com/LGLbkS0D7l

— 因幡めぐる@競技プログラミング (@meguru_comp) 2016年2月9日

３. コンテストが楽しい

やっぱり人間なので競う場があったほうが盛り上がるんですね、AtCoderでは時間内に複数の問題を解くコンテスト（代表的なのはAtCoder Beginner Contest、通称ABC）がなんと週一で開かれています。最近見れてないけどコンテスト後に他の人の賢い解法ツイートや感想ツイートを見るところまで含めてコンテストだと思ってる。

他にもレートの上下があるのが楽しいとか色んな意見がありますが私が競プロを楽しいと思う理由はこんな感じです。あと競プロは授業の役に立つ、競プロは研究の役に立つ！（いいえ）

３. 何から始めればいいのか

こっからは具体的な話です、ぶっちゃけ最低限の検索力とプログラミング経験があれば読まなくてもいいかもしれない、調べるのめんどくさい人だけ読めば良さそう。

まず、AtCoderに登録しましょう。
atcoder.jp
この時についでにTwitterで競プロ垢とか作ってしまうといいかもしれない。

さて、ここからは言語選択です、授業で習ったC言語、Pythonを含め色々ありますがここではC++をおススメしたいです。理由としては

• 速い（実行時間が少なくて済む）
• ネットで競プロの解説記事としてC++が使われていることが多くわからないことを調べやすい。
• 少なくともC言語よりは楽に書ける（STLの関数やクラスの存在）。
• 抽象化が便利、特に他人のライブラリをパクる時に。

そして何よりもAtCoderの公式C++入門教材、APG4bの存在が大きいです。
atcoder.jp
何を隠そう私も競プロもといプログラミングそのものにここから入門しました。プログラミング初心者にもわかりやすくC++について説明されています、節ごとに演習問題があるのも嬉しい。特に競プロをやる言語にこだわりがない人は、C++でやってみるのはいかがでしょうか？

APG4bのレベルについてざっくり触れると、

• 1章：基礎基礎、ここは全部理解するようにしましょう、コンテストに出るのもここ全部終わってから。
• 2章：難しい、1章とのギャップがえぐい、特に2.04.参照、2.05.再帰関数はいきなり全部理解しようとすると相当骨が折れる.....、と思ったけどソフⅠのスピードを考えると学科民にはそんな難しくないかもしれん、ポインタもやってるしね。私は受験直後のずっと暇なはずの時期を使ってもここを理解するのに3週間かかりました。
• 3章：なんか今までと違って機能一覧みたいな感じ、どんなことが出来るのかだけ目を通しておいて実際の問題で使えそうだと思った時に戻ってきて都度読み返すのがいいと思ってます。
• 4章：3章と同じく機能一覧だけどよりadvanced、読んでなくても青くらいにはなれるけど4.03.テンプレートくらいは読んでおくと自分でライブラリを作りたくなった時に便利なのかもしれない？......（人のライブラリパクるばっかで自分で作ったことない人）。

みたいな感じです。わかると思いますが完全主観。

４. 次に何をすればいいか

APG4bがある程度終わった（決して全てではない）後に何すればいいかの個人的オススメは冒頭にも貼った以前の記事にも書いたので省略します。宣伝は(ry
mogurin1000000007.hatenablog.com
ただこれ書いた後に一つかなりオススメの教材が出来てたのでそれだけ紹介します、その名も競プロ典型90問。
atcoder.jp
怖いくらい競プロに必要な知識がギュッと詰まった濃縮還元率1000000007%くらいの超良問集です、下手な過去問埋めするより余程効率的にアルゴリズム力（あるごりずむちから）を鍛えることが出来ます。注意点としては決して簡単な問題ではないので自分に合った難易度のものを選んで解いていくことをお勧めします。
ちなみにこの問題集作ったの弊学のB1らしいですよ、近々本も出すらしい、怖くて泣いちゃった。

実は環境構築周りの話はどこにも書いてないんですがこれは私も未だに人に説明できるほど自分のIDEがしっかりしてない、だれかonline-judge-toolsの使い方教えてくれ。

５. 最後に

競プロをやりましょう
競プロをやりましょう
競プロをやりましょう
競　プ　ロ　を　や　り　ま　し　ょ　う
※学業との兼ね合いは程々に

APG4bからAtCoderを始めた人向けの導線

※この記事は弊学で最近競技プログラミングを始める人が急に増えているのを観測したので急ごしらえでこさえたものです。荒い上に間違っている部分も多いと思うのですがご了承ください。暇なときに手直しはする、多分。

０. はじめに

　APG4bはAtCoderが提供しているC++の入門教材ですが、ここから入った人向けの導線があんまり整備されてない気がしたので自分なりに有用そうなサイトとか記事とかもろもろをまとめておこうと思いました。もちろん完全主観なので絶対正しいわけではありませんが、私が競プロを始めたときにはAtCoderという環境に慣れるためにかなりの試行錯誤を要したので、その苦労の一部でも後から始めた人は軽くなればいいなと考えています。

１. APG4b

　APG4bから始めた人向けとか謳ってるのでまず最初に軽くAPG4bについて触れます。ぶっちゃけ難しいです。個人的な感触としては

• 1章: 必要最低限、コンテストに挑むならまずはここまではやる、精進もここまでは終わらせてからにする。
• 2章: いきなり難易度爆上がりする。ここまで完璧にできるならぶっちゃけ緑まではかなり早い段階でいけるはず、精進もこのあたりから始めるのが良さげ。
• 3章: 難易度が高いというよりC++の"機能"の部分が多い気がする、コンテストで戦う上では必須の知識も多いが大概D問題以降。
• 4章: わ　た　し　が　ま　だ　理　解　し　て　い　な　い、やんなくても青にはなれます。

特に2.04、2.05、3.04は他のに比べても難易度が2段階くらい高いです、詰まるようならあまり無理をせず一度飛ばすことをおすすめします。緑くらいになってから学びなおしても遅くはないはず。また、3章は基本的に覚えることが多く、全部を一辺に暗記しようとせず、最初のうちはどんな機能があるのかだけ覚えておいて、実際に使いそうな問題になったら該当の節に戻ってきてそれを見ながら問題を解くとかでいいと思います。その内基本的なのは自然と覚えてすらすら出てくるようになります。後サラッと書いちゃったけど緑とか色が出てきたらAtCoderのマイプロフィールで確認できるレートの色のことです灰→茶→緑→水→青→黄→橙→赤の順でレートが上がってきます。まずは半分、水を目指そう！とか勢いで見積もるとちょっとやばいことになるのでご注意を...（体験談）。

APG4bについてはこんなもんだろ、知らんけど

ある程度APG4bを終えた後は？

　この後はぶっちゃけ人によって精進の仕方もコンテストに対する姿勢も全然異なるので本当に基本的なところだけまとめていきます。

AtCoder Beginners Selectionをやってみる

　言わずと知れた、AtCoderの登竜門、AtCoder Beginners Selection
atcoder.jp
問題ごとに競プロで必要なアルゴリズム（というよりもはや基本姿勢）である全探索や貪欲（Greedy）を学べる良問集、簡単な問題が多いのは確かだが、これをしっかりと意識して解いておくと後が楽、あの時の僕にだれか教えてあげて。
解説も貼っておきます。
qiita.com
この記事を書かれているけんちょん（ブログではdrken）さんは、AtCoderから競プロを始める人は大変お世話になるので覚えておきましょう。ぶっちゃけ緑になるくらいまではこの方の記事におんぶにだっこになるはずです、適当なアルゴリズムの後ろにこの方の名前つけて調べると大体何らかの記事出てくる、多分。

AtCoder Problemsに登録する

　AtCoderの過去問やるなら何といってもここ！知っていると知らないとでは精進のストレスが大きく違うというかこれ知らないで精進してる人は多分いない。今日もみんなkenkooooさんに感謝しよう。

Boot camp for Beginnersをやる

　AtCoder ProblemsのTrainingの欄から進むことが出来る。私はあまりやってないので強くお勧めできないのですが、やってる人からの評判はいい。Easy/Medium/Hardで各々100問ずつの問題が用意されており、自分に合ったレベルを選んで進められる。

ABCの○○埋めをやる

　○○にはAとかBとか問題番号が入ります。Tableで縦一直線に並んでるので精進がしやすいんですね、効果的かと言われると、どうだろう...。でもやってる人は結構見かけます。

色埋めをやる

　各問題には難易度に合わせて色が付けられてるので、特定の色の問題を全部解くつもりで片っ端からやることです。私はこれをやってました、実は量のわりに効果がものすごく高いわけではなさそうです。けど一つの手段としては有効かなーと思ってます。注意点としては試験管問題はやらなくていいと思います、実装が重いわりに学べるところのある問題が少ない。

AtCoder Problemsの基本的な使い方ってこんなもんだろうか、他にもいろんな機能があるので色々いじってみましょう、かなり便利です。あと、AtCoder ProblemsだけにとどまらずAtCoderを楽しむためのサイトはたくさんあります。次の記事
noimin.hatenablog.com
によくまとまっていたので一回目を通しておくのをおすすめします。

Twitterを始める

　競プロをやるにあたり欠かせないツールになりつつあります。フォローした方がいい人がまとめてあるものとして、AtCoderの社長さんのブログ
chokudai.hatenablog.com
を引用しておきますが、個人的に初心者が絶対フォローしておくべき人として 競技プログラミングをするフレンズ さんを上げておきます、なぜかと言いますと最初のうちはAtCoderのコンテストの解説は結構読みにくいです。解説放送もしているのでそちらを見ることも大事なのですが、もっと手軽な方法としてコンテスト後に大抵フレンズさんが問題に関する簡単な解説ツイートをしてくれることが多いので、それを読むだけで大分ためになります。
　他に自分と近い色の人をフォローして刺激にしたり、色の上の人をフォローして色々学び取ったり、使い方は人次第ですがいずれにしろかなり重要です。わからないこともTwitterに投げると質問に答えてもらえたりする、嬉しい。

Google拡張機能を入れる

　AtCoderには有志による様々な拡張機能があるので使えると便利です。こちらの記事
dailylife.dev
にある程度まとまってました、どれも便利です。

他人の色変記事を読む

　先人の歩んだ道が参考になるのは当たり前、AtCoder　入茶/入緑/入水記事あたりで調べるとたくさん出てきます。学んだ方がいいアルゴリズムの一覧とか載せてくれている人もいる。私も入水記事書いてるから読んで（宣伝）（本音を言うと本来ここに書いた方がいいことでダブってる内容があるけどもっかい書くのだるいからこっち読んで適宜補って）
mogurin1000000007.hatenablog.com

よし、こんなところで...、ぶっちゃけこの記事かなり色々欠けてる気がするんですが今ちょっと他のやりたいことがあって頭回らないんで後日色々手直しするかもしれない、なんか他に書くべき内容あったらじゃんじゃん指摘してください、ここまで読んでいただきありがとうございました。

青色になりました

は、おい俺は...というほどでもないな、青変しましたわーい pic.twitter.com/hN9cnlzOID

— mogurin (@mogurin_kyopro) 2021年1月10日

お久しぶりです、mogurinです。この度ABC188にて入青を果たしました、やったね！！

０. いつもの

いつものやつです、いやいつものとか言いながらこれやるの初めてなんですけど他の人やってるんでとにかくいつものやつです。




他の人に比べると少し精進は少なめ？春休み入ったら少し時間できると思うんで頑張りたいですね、でもエロゲの誘惑に負けないかが不安だな。

１. 水->青で新しく身に着けたアルゴリズム

• マージテク

くっつけるときに、大きい方に小さい方をくっつければ、毎回サイズが2倍以上にはなって、計算量がlogで抑えられる〜って話だとざっくり思ってます

— nok0 (@nok0_kyopro) 2020年11月15日

天才かよ

• ダブリング

algo-logic.info
前々からやらなきゃなーと思ってたダブリングを履修しました、わかってみれば簡単かつ汎用性のある知識だった。

• 部分集合の全列挙

ark4rk.hatenablog.com
青になってから覚えたのでここに入れていいか微妙だけど感動したから入れた、天才かよ(2回目)

Q. ところで、これらのアルゴリズムをコンテスト中に実際に使う機会はありましたか？
A. いいえ
マージテクなんかはむしろコンテスト終わってから教わった感じですね、しゃーない。どちらかというとAtcoder Libraryとかをたくさん使う機会があったので新規のアルゴリズムよりもデータ構造に慣れたことの方がデ/ア面の成長としては大きい気がします。

２. 水->青になるまでにやったこと

• 今までの知識の復習

大学でAtcoderの問題を使って初歩のアルゴリズムを教えてくれる授業がありまして、ぶっちゃけ単位と点が欲しくてとったのですが、結果的に知識を復習することになりました、それがために...なった...のかなぁ？あんまり関係ない気もする。

• 毎回コンテストに出る

ABCもARCもAGCも大体出た、偉い！！

ここだけの話水の時から何か特別にやったこと、ないんですよね...。後述しますけど多分青変できたのはパチンコで当たり台引いたのが大きそう...。

３. 水->青になるまでの過程

急上昇期

急上昇期

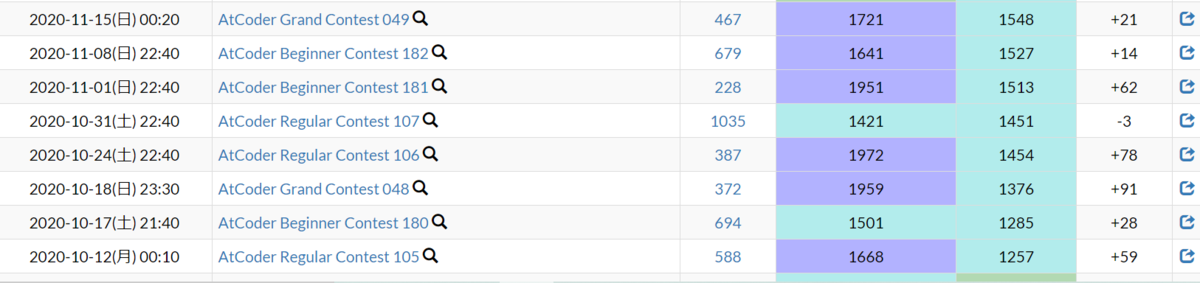
パチンコ当たり台連発時期、なんか面白いくらい青パフォが出た。

急落期

急落期

コンテスト2回で-99になりました、Foxてめぇだけは許さねえからな...。
競プロ辞めたくなるとかそんなことは特になく、まぁうまく行き過ぎてたから補正だろみたいに捉えるようにしてました、決してショックでポテチ爆食いしたりしてない。

停滞期

停滞期

下がるわけではないけどなんかぱっとしなかった時期、ただこの辺りからABCが目に見えて易化してた(具体的にはFがなんか典型っぽくなった)のでうまくクリティカル出せば一気にいいパフォが出そうな予感があった、実際ABC185で初の全完したりもした。

入青

入青

うまく考察がハマったり既出問に当たったりして、全完黄パフォ2回で無事入青、やったぜ！！

４. 意識していたこと

そろそろ早解きにも意識を向ける

さっっっっすがに全く早解き要素を気にしないわけにはいかなくなってきたのでひとまずA~D問題を問題読みながら入力部分を書くとか、「早く解こう！！」と思って解くようにしてます、するとちょっと早くなる(ほんとか？)。

天才になる

私は天才私は天才私は天才私は...

はい、前にも書いた奴ですね、自分を天才と信じ込むとなんかうまくいく！、かも。その分失敗したときのダメージもでかくなるからほどほどにやろう。

コンテストでその都度新規の知識をつける

個人的に解けてない問題の解説はあまり読みたくない人なんですが、コンテスト終了後のTLを眺めてるとなんとなく自分の知らない知識が必要だったかどうかがわかります。その時は潔く解説を見る、もしくは必要な知識を他の人に聞くようにしてました。SPJのみなさんいつもありがとう。

こーんな感じですかね、書き忘れたことあったらあとで追記しよ

５. ここからやりたいこと

• 水埋め、青埋め

ちらほら精進不足のぼろが出始めてる気がするので春休み使ってなんとか精進したい...。

• 環境構築

せっかくインストールしたVSCodeがただのライブラリ置き場になってるのでちゃんと動くようにしたい...。これも春休み中に他の人に聞いたり調べたりしながらだな。

黄色はおそらく一筋縄ではいかなそう...。なんとか今年中に暖色コーダーになることを目指して頑張っていきたいです。

６. 最後に

ひとまず寒色の中では一番上の色になれて自分の中で一区切りついたかな、という感じです。ここからはより一層厳しい戦いになっていきそうですが、まぁ趣味として楽しんでいるのでほどほどに頑張っていきたいです。また今年中に黄変記事を自分が書いてればいいな～、なんて。何はともあれ、ここまで読んでいただきありがとうございました。

７. 余談

祝いの言葉ににこにこしております pic.twitter.com/cVWxxyIfsn

— mogurin (@mogurin_kyopro) 2021年1月10日

もぐりんのアイコンめちゃくちゃ不評でウケる(私も嫌い)

— nok0 (@nok0_kyopro) 2021年1月12日

よし、ツイートした or いいねしたアカウント覚えた。月夜ばかりと思うなよ...？(ちなみにこの後アイコン画像をマイナーチェンジした)

ABC184E Third Avenue

問題

S,G,.,#,a~zからなるのグリッドが与えられます。この時、#は入ることができないマス、a~zはテレポーターのあるマスを表します。この時、次の規則に従って移動するときSからGへは最短何手で移動できるか求めよ。

1手で次のどちらかの移動が可能である。

• 現在いるマスと上下左右で隣接しているどれかの#以外のマスに移動する。

• 現在いるマスがa~zのマスであるときにのみ可能である。同じ文字の書かれたマスに移動する。

制約

考え方

テレポートでグラフ上に新しい辺が増えただけなんだから愚直に同じ文字のマス同士に辺を張ってBFSでOK！！

どうして...

よく考えると例えばグリッド上の半分が全部aだったりするとa同士に張られる辺の数がになって破滅することがわかります。TLE出た瞬間にダメなケース思いつくことってあるよね...

コンテスト中はただのBFSをバグらせてたこともあり(は？)、残り時間もなかったんでここで終わったんですが、うーーんとうなってると、"同じ文字が書かれているマスをすべて一つのノードにまとめてしまう"アイデアを思いつきます。天才だな―
と思ってたんですけどこの方法だとテレポーターを使う時と単純にそのマスを通過するときの区別ができません。ダメかー
またうんうん唸ってると"同じ文字のマスをつなぐ超頂点を作る"ことでその超頂点を通過するときにだけコストがかかるようにすればいいことに気付きます。なるほどなー

ここまで思い浮かべは後は01-BFSなりDijkstraなりで実装できます。結構シンプルな解法だけにコンテスト中に思い浮かびたかったなー

コード

今回は01-BFSで実装してみることにします。

#include <bits/stdc++.h>
using namespace std;
#define rep(i,n) for (int i = 0;i < (int)(n);i++)
using ll = long long;
const long long INF = 1LL << 60;

template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return true; } return false; }
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return true; } return false; }

ll dp[4010000];


int main()
{
  ll H,W; cin>>H>>W;
  vector<vector<ll>> graph(H*W+26,vector<ll>(0));
  vector<string> grid(H); rep(i,H) cin>>grid[i];
  
  //テーブル初期化
  rep(i,H) rep(j,W) dp[i*W+j]=INF;
  for(int v=H*W;v<H*W+26;v++) dp[v]=INF;
  
  auto f=[&](ll i,ll j){
    return i*W+j;
  };
  
  //graph作成
  rep(i,H) rep(j,W) {
    if(grid[i][j]=='#') continue;
    if(i<H-1&&grid[i+1][j]!='#') {
      graph[f(i,j)].push_back(f(i+1,j));
      graph[f(i+1,j)].push_back(f(i,j));
    }
    if(j<W-1&&grid[i][j+1]!='#') {
      graph[f(i,j)].push_back(f(i,j+1));
      graph[f(i,j+1)].push_back(f(i,j));
    }
    
    if(grid[i][j]=='.'||grid[i][j]=='S'||grid[i][j]=='G') continue;
    
    graph[H*W+grid[i][j]-'a'].push_back(f(i,j));
    graph[f(i,j)].push_back(H*W+grid[i][j]-'a');
  }
  
  //sとg
  ll s,g;
  rep(i,H) rep(j,W) {
    if(grid[i][j]=='S') s=f(i,j);
    if(grid[i][j]=='G') g=f(i,j);
  }
  
  //01-bfs
  deque<ll> deq;
  deq.push_back(s);
  dp[s]=0;
  while(!deq.empty()) {
    ll v=deq.front(); deq.pop_front();
    for(auto nv:graph[v]) {
      if(nv<H*W&&chmin(dp[nv],dp[v]+1)) deq.push_back(nv);
      if(nv>=H*W&&chmin(dp[nv],dp[v])) deq.push_front(nv);
    }
  }

  cout<<(dp[g]==INF?-1:dp[g])<<'\n';

  return 0;
}

感想

テレポーター部分をどう処理するかが鍵な問題でしたね、十分に考察時間が取れれば思いつけた自信はあるので、ただのBFSとかをバグらせないようにしたい...、それともライブラリ化したほうがいいかなぁ。
それはそれとして"共通のノードをつなぐ超頂点を作る"のはふつうに典型っぽいのでこの機会に覚えておきます。ここまで読んでいただきありがとうございました。

余談

某discordにて
僕「いやー、こういうのをぱっと思いつけるようになりたい」
？？？「え、これは典型」
？？？「まぁ典型」
？？？「うん」
精進不足です、すいませんでした...
？？？「まぁPASTで既出だったんだけど」
それはダメだろAtcoder

ABC184D increment of coins

問題

袋の中に金貨が枚、銀貨が枚、銅貨が枚入っています。この時、どれかの硬貨が100枚になるまで次の操作を続けます。

• 袋の中の硬貨をランダムに1枚取り出し、同じ種類の硬貨を2枚戻す。

この時、操作回数の期待値を求めなさい。

制約

考え方

期待値、ほい来た線形性！！...あれ？
はい、この問題貨幣一枚取り出すごとにその確率が前の各々の硬貨の枚数に依存するし終了時点での硬貨の総枚数が状態によって異なるので線形性使おうとすると破滅しますね、困ったな―
コンテスト中にほんとに困ったのでとりあえず「期待値　競プロ」あたりで検索してみます。

ひとまず検索は基本

んー、やっぱり線形性が基本ぽいしなんか問題をうまく読み替えればいいのかなー、うん？

D...P...？
制約から状態の種類はくらい...、そしてD問題...(その当てはめ方はどうなんだ)
はい、見えましたね、DPで解けそうなことがわかったらあとは遷移を考えるだけです。

解法1

私がコンテスト中に考えた解法です。金貨の数が枚、金貨の数が枚、金貨の数が枚となる確率をdp[a][b][c]とすると、遷移が配るDPでうまく書けそうです。すなわち、

dp[a+1][b][c] += dp[a][b][c]*(double)a/(a+b+c);
dp[a][b+1][c] += dp[a][b][c]*(double)b/(a+b+c);
dp[a][b][c+1] += dp[a][b][c]*(double)c/(a+b+c);

と書けますね、後は操作1回ごとに硬貨の総枚数が1枚ずつ増えることを考慮すると、のどれか一つのみがである状態のとdp[a][b][c]の積を各々足すことで期待値が求まります。

解法1コード

#include <bits/stdc++.h>
using namespace std;
#define rep(i,n) for (int i = 0;i < (int)(n);i++)
using ll = long long;


double dp[110][110][110];

int main()
{
  cout << fixed << setprecision(15);

  ll A,B,C; cin>>A>>B>>C;
  dp[A][B][C]=1.0;
  
  for(int a=A;a<=100;a++) for(int b=B;b<=100;b++) for(int c=C;c<=100;c++) {
    //a,b,cのいずれかが100ならその時点で遷移終了
    ll count=0;
    if(a==100) count++;
    if(b==100) count++;
    if(c==100) count++;
    if(count) continue;
    
    dp[a+1][b][c]+=dp[a][b][c]*double(a)/(a+b+c);
    dp[a][b+1][c]+=dp[a][b][c]*double(b)/(a+b+c);
    dp[a][b][c+1]+=dp[a][b][c]*double(c)/(a+b+c);
  }
  
  double ans=0;
  for(int a=A;a<=100;a++) for(int b=B;b<=100;b++) for(int c=C;c<=100;c++) {
    //a,b,cのいずれか1つのみが100の状態の確率だけ考える。
    ll count=0;
    if(a==100) count++;
    if(b==100) count++;
    if(c==100) count++;
    if(count!=1) continue;
    
    ans+=((a+b+c)-(A+B+C))*dp[a][b][c];  
  }
  
  cout<<ans<<'\n';
  return 0;
}

解法2

俗にいう期待値DPというやつですね。dp[a][b][c]を金貨が枚、銀貨が枚、銅貨が枚から始めたときの期待値と置くと、今度は貰うDPできれいに書けますね。すなわち

dp[a][b][c] += dp[a+1][b][c]*(double)a/(a+b+c);
dp[a][b][c] += dp[a][b+1][c](double)b/(a+b+c);
dp[a][b][c] += dp[a][b][c+1](double)c/(a+b+c);
dp[a][b][c] += 1.0;

うーん綺麗、しかもこの解法だと最後に合計する手間がないのでぱっと思いつけるのならこっちのほうが良さそうですね。思いつけるようになりたい...。
どの問題かは言わないでおきますが期待値DPはEducational DP Contestでも扱われていたので、うん、やっぱり典型として使いこなせるようになっておこう。

解法2コード

#include <bits/stdc++.h>
using namespace std;
#define rep(i,n) for (int i = 0;i < (int)(n);i++)
using ll = long long;

double dp[110][110][110];

int main()
{
  cout << fixed << setprecision(15);

  ll A,B,C; cin>>A>>B>>C;
  for(int a=99;a>=A;a--) for(int b=99;b>=B;b--) for(int c=99;c>=C;c--) {
    ll s=a+b+c;
    dp[a][b][c]+=dp[a+1][b][c]*(double)a/s;
    dp[a][b][c]+=dp[a][b+1][c]*(double)b/s;
    dp[a][b][c]+=dp[a][b][c+1]*(double)c/s;
    dp[a][b][c]+=1.0;
  }
  
  cout<<dp[A][B][C]<<'\n';
  
  return 0;
}

感想

最近期待値/確率DPがABCで出ていなかった(もしかしたら私が参加し始めた3月から考えると初？)ので頭から抜け落ちてて手間取りました。検索したらすぐに出てきたからよかったものの精進しないとですね...。読んでいただきありがとうございました。

ABC184C Super Ryuma

• 問題リンク

問題

無限に広がるグリッド上の指定された二つの座標

の間を次の規則に従って駒を移動させる際に、必要な最小手数を答えなさい。

駒は一手で次の条件のどれかを満たすからへのが可能である。

• ...(移動A)
• ...(移動B)
• ...(移動C)

制約

• 

考え方

この問題が茶diffなのは正直びっくりしました。そんなに簡単な場合分けかなぁ。
とりあえず問題をみてぱっと思いつくことは、

• AとBの移動を一回ずつ行うことでパリティの等しいマスには最大手で移動できる。
• 上の移動にさらにCの移動を行うことで最大手で全てのマスに移動ができる。

ですね。つまりどのマスにも手以内で移動できることがわかりました。ならば答えとしてあり得るのはの高々つしかないんだから場合分けでいけるはず。さらに少し考えれば手なのは当然動かない時、手なのは上のA,B,Cのどれかの条件を満たす時なので、手の時を場合分けできれば問題が解けたことになります。

ここで解説では手で移動するときを丁寧に場合分けすることで求めているのですが、ここでは少し異なる解法で解いてみます。使用する典型は
"ある対象への条件を別の対象の条件に読み替える"
です。最近だとABC181F Silver Woods
atcoder.jp
が、"障害物の点にかぶらないように半径の円を動かす"を"点を半径の円の障害物と被らないように動かす"、に読み替えることで解く問題でした。「動かす点」に関する条件を「障害物」に関する条件に読み替えてしまうのですね。

さて、今回の問題では
"からに手で移動できるかどうか"
を
"から手で移動できるマスにから手で移動できるマスが存在するかどうか"
に読み替えます。"からの移動"に関する条件を一部"からの移動"に関する条件に読み替えてしまうわけです。

ここで一番単純な方針は
"から手で移動できるマスを全列挙してしまい、これらの中で一つでもからの移動に関するA,B,Cの条件のどれかを満たすマスが存在するかどうか求める。"
です。ただこれには問題があってから手で移動できるマスって無限にあるんですよね、どうしよっかなー。

ここで図とじーっとにらめっこすると
"からA,Bどちらか手で移動できるマスの中にからの移動に関するA,Bの条件のどちらかを満たすマスが存在する"
が、先ほど考えた
"とのパリティが等しい"
と同値であることがわかります。ならばあと考えるべき手の移動は二つ、

• A→C、B→C、C→A、C→Bの移動
• C→Cの移動

つじゃん！！(すいません)、ともあれどの移動にもCの移動が含まれており、なおかつA→CとC→A、B→CとC→Bの移動で行けるところは各々実質変わらないことに気付けば、これらの移動については
"からCの移動手で移動できるマスを列挙してしまい、これらの中で一つでもからの移動に関するA,B,Cの条件のどれかを満たすマスが存在するかどうか求める。"
ことで判定可能であることに気づけます。いやー中々に骨の折れる問題だった。

コード

#include <bits/stdc++.h>
using namespace std;

#define rep(i,n) for (int i = 0;i < (int)(n);i++)
using ll = long long;

//移動の条件を全て関数化してしまう
bool can_reach(ll a,ll b,ll c,ll d) {
  if(a+b==c+d) return true;
  if(a-b==c-d) return true;
  if(abs(a-c)+abs(b-d)<=3) return true;
  
  return false;
}

int main()
{
  ios::sync_with_stdio(false);
  cin.tie(nullptr);
  // cout << fixed << setprecision(15);

  ll r1,c1,r2,c2; cin>>r1>>c1>>r2>>c2;
  //移動が0手の時
  if(r1==r2&&c1==c2) {
    cout<<0<<'\n';
    return 0;
  }
  //移動が1手の時
  if(can_reach(r1,c1,r2,c2)) {
    cout<<1<<'\n';
    return 0;
  }
  //パリティが等しいとき
  if(~(abs(r2-r1)+abs(c1-c2))&1) {
    cout<<2<<'\n';
    return 0;
  }
  //(r2,c2)からCの移動1手で行けるマスが(r1,c2)から1手の移動で到達可能な時
  for(int i=c2-3;i<=c2+3;i++) for(int j=r2-3;j<=r2+3;j++) {
    if(abs(i-c2)+abs(j-r2)>3) continue;
    if(can_reach(r1,c1,j,i)) {
      cout<<2<<'\n';
      return 0;
    }
  }
  //それ以外は3手
  cout<<3<<'\n';
  
  return 0;
}

感想

やっぱ難しいよこれぇ、場合分け問題は総じて苦手な僕ですがそれでもこれが茶diffはおかしいだろ、インフレは日々加速してるんですね...。精進せねば。ここまで読んでいただきありがとうございました。

ARC108C Keep Graph Connected

• 問題リンク

問題

頂点辺の"多重辺を含む"連結なグラフが与えられる。この時辺にはラベルが各々貼られているので、すべての頂点に以上以下の整数を書き込むことで、

"辺の両端の頂点に書き込まれた整数のうち片方のみが辺に張られたラベルと等しい辺のみを残したグラフが連結のままである"

ことが可能であるか判定し、また可能ならそのような整数の書き込み方を1つ上げなさい。

制約

与えられるグラフに自己ループはない

考え方

「連結グラフの辺削除、ってことは全域木！」、とここまではコンテスト中に考えが及んだんですが最初に思いついた方針が

"根を決め打ちして、各頂点について、根なら自分とつながっているすべての辺のラベルと異なる整数、それ以外の頂点は親とつなぐ辺のラベルの整数を書き込む"

というのが解法かなと思ったんですがこれは例えば

というテストケースで落ちます。つまり同じ頂点をはさんで同じ整数のラベルが張られた辺があるとダメなわけですね。

ここでコンテスト中はいい案も浮かばずdpっぽくて面白そうな問題Dに逃げてしまったのですが、実はこれ

"根のみ適当な整数をいれて、他の頂点については親の頂点に書かれた整数が、自分と親とを結ぶ辺に貼られたラベルの整数と等しかったら自分の頂点にはそれ以外の適当な数を書き、等しくない場合は自分の頂点に辺に貼られたラベルの整数を書く"

という方針でいいんですね、うーん思いつかなかった。根から貪欲に決めるという部分は一緒なので、後は実験とかして気づきたかったですね。

コード

https://atcoder.jp/contests/arc108/submissions/18293471

感想

コンテスト中の問題の取捨選択は難しいのでそれ自体をミスったのはやむなしですが、最初の嘘解法時点でも'No'になるケースはないのわかりそうなものなのに気づけてなかったのがダメですね、ここに気付いてればもう少しCに時間割こうと思えていたかもしれない。反省です。後コンテスト中に直感的にそんな気がしてただけで

"連結な無向グラフを考える時は全域木を疑う"

も別に典型として知ってたわけじゃなかったのでこれも改めて覚えなおします。読んでくれてありがとうございました。